Research

  /  

Application Areas

Biological Systems & Mathematical Biology

Ever better experimental techniques allow to perform experiments under tightly controlled conditions and can deliver gigantic amounts of data reflecting the complexity of biology. This has vastly increased the importance of mathematical and computational descriptions of biological systems. Thus, quantitative biology is a major research thrust in ESAM. Much of that research is done in connection with the NSF-Simons National Institute for Theory and Mathematics in Biology (NITMB).

Faculty

Daniel Abrams	Luís Amaral	Alvin Bayliss
David Chopp	William Kath	Madhav Mani
Niall Mangan	Michael Miksis	Hermann Riecke
Petia Vlahovska	Vladimir Volpert

Recent publications

Jump to a Section

• Biofluid mechanics
• Developmental biology
• Computational Ecology
• Genomics
• Neuroscience

Biofluid mechanics 

Biofluid mechanics is the subject of applying fundamental ideas from fluid mechanics to better understand the biology of living systems. This is a field that is moving very rapidly today because of the development of new experimental techniques that have allowed for quantitative measurements of specific biological systems, e.g., the motion of a cell.

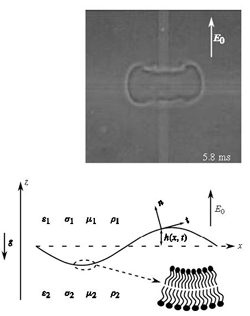
Research within ESAM involves the development of mathematical models of interesting biological systems, the development of new analytical and computational methods to solve these models, and interaction with experimental groups to verify the validity of the investigation. Specific areas of current research include biofilms (an aggregation of bacteria on solid surfaces surrounded by gas or liquid), vesicle and cell dynamics, and the dynamics of aneurysms.

Core Faculty
M. Mani, M.J. Miksis, P. Vlahovska

Return to Top

Developmental Biology

The correlation of organismal form and function is one of the central themes in biology, and the outcome of a developmental process—morphogenesis. While the zoo of organismal form seems limitless, we expect there to be unity in processes and mechanisms that give rise to them.

In analogy with the morphogenesis of our planet, while the details of the current shape of continents depends on time and historical contingency, the mechanisms that drive tectonic plates and the flows in the Earth's core are far more general. What are the underlying principles and mechanisms that drives the emergence of organismal form? This is the central question driving our research.

Our work explores two avenues of research: 1) Solving data-driven, inverse-problems that allow us to make measurements of physical forces and chemical kinetics that experiments do not give direct access, and 2) in close collaboration with experimentalists, we combine measurements made in their labs with ours to guide the development of mathematical models that are phenomenological in nature and formalize our intuition for how the physical properties of polymers, cells, and tissues emerges from, and constrains, the biological process of interest.

Core Faculty
M. Mani, N. Mangan

Return to Top

Computational Ecology

Computational ecology is the study of ecological communities using mathematical techniques. 

One important problem in computational ecology is to study interactions among different species comprising the community, say one consisting of N species. The objective is to be able to predict how the community evolves in time and how it responds to changes in ecological conditions. The members of the community can interact among themselves (intra-species interactions) or with members of other species (inter-species interactions). 

Intra-species interactions can be competitive, i.e., competition for scarce resources, food, water or living space, or can be positive where members of the community help each other (think of wolf-packs). Interspecies interactions will generally involve both some form of competition between the different species coupled with predation, so that some species (predators) gain from interacting with others (prey). 

One very important competition scheme involves cyclic competition. Suppose the community consists of N= 3 species, call them u,v and w. Suppose v has a competitive advantage over u, w has a competitive advantage over v and u has a competitive advantage over w (thus closing the cycle). Such competition schemes occur across many different scales of life, (e.g., bacterial,plants and animals), and can be considered as nature playing the children’s game of Rock-Paper-Scissors - v wins over u (rock crushes scissors),w wins over v (paper covers rock) and u wins over w (scissors cuts paper). As with the Rock-Paper-Scissors game, the winner cannot be predicted in advance. (Such competition schemes are sometimes referred to as “winnerless”.) These communities can exhibit a range of fascinating dynamics including, but not restricted to, heteroclinic cycles where each species has a period of dominance over the whole community for increasingly long times. 

In addition, cyclically competing communities can exhibit a wide array of spatial patterns. As just two examples, see the single spiral and then the multiple spirals that can form among a RPS community (colors correspond to concentrations of the three different species).

This is just one example, other behaviors (even more complex) are possible for communities with N >3 . In the department we have an extensive program in population dynamics, pulling together computation, analysis and asymptotics. 

 

Core Faculty:
A. Bayliss, M. Mani, V. Volpert

Return to Top

Genomics

Having access to the genome of an organism is similar to having a primitive understanding of a language's alphabet without understanding what words mean and how sentences are structured. While there is no shortage of data flowing in from single-cell sequencing experiments, we are missing our Rosetta Stone to help make sense of it all.

This is perhaps the most pressing challenge in quantitative biology and biomedicine, and groups in ESAM are using tools from statistics, machine learning, and statistical physics to build data-driven mathematical models to address it.

Core Faculty
W.L. Kath, M. Mani

Return to Top

Neuroscience

The brain is exceedingly complex, from the sub-cellular biophysical processes that control individual neurons and their communication to the intricate neuronal networks characterizing individual brain areas and their mutual interactions. To unravel the function of the brain at these different levels mathematics and computation bring an exciting, extraordinarily wide range of concepts and tools to bear, like ordinary and partial differential equations, stochastic processes, agent-based modeling, statistics, ... just to mention a few.

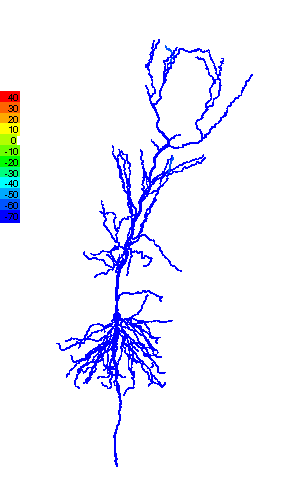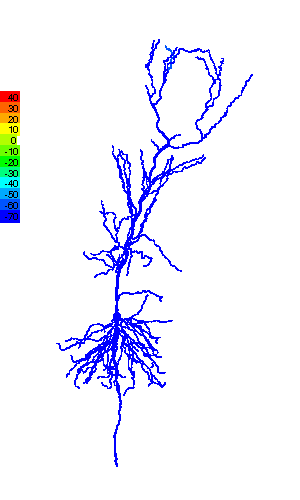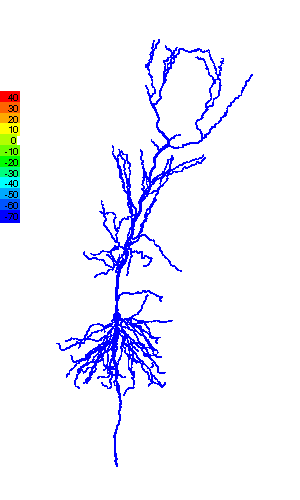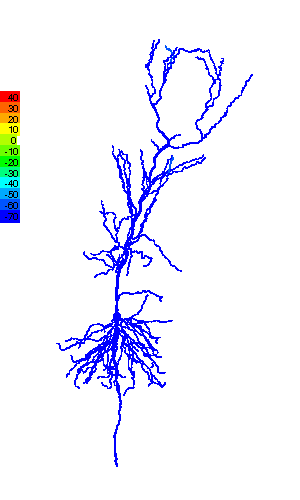
Research in ESAM identifies the functional relevance of the complex shape (morphology) that characterizes many neurons (Fig.1) and the computational modeling provides valuable information about quantities that are experimentally not accessible, e.g. ion concentrations. Such modeling helps obtain a more complete picture of the dynamics of individual neurons and their function in neural circuits. That, for instance, control the motion of a fly in response to temperature variations (Fig.2).

 

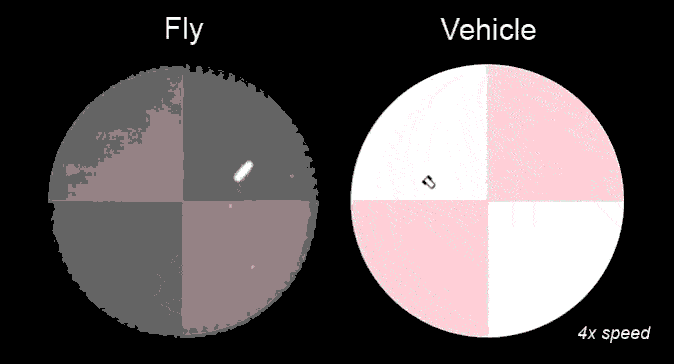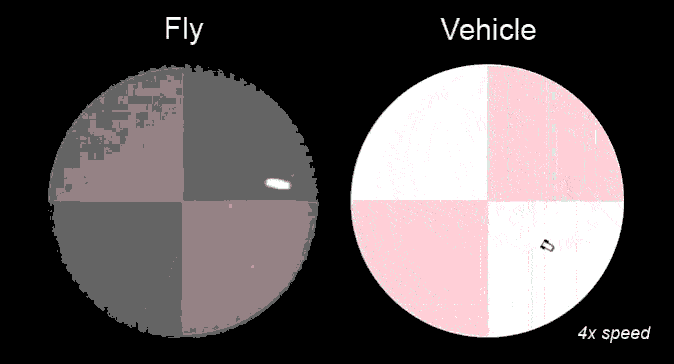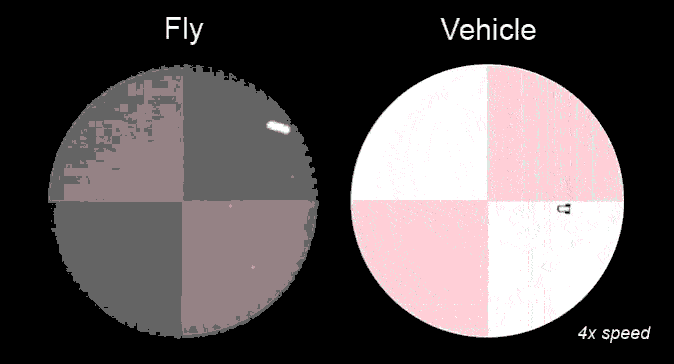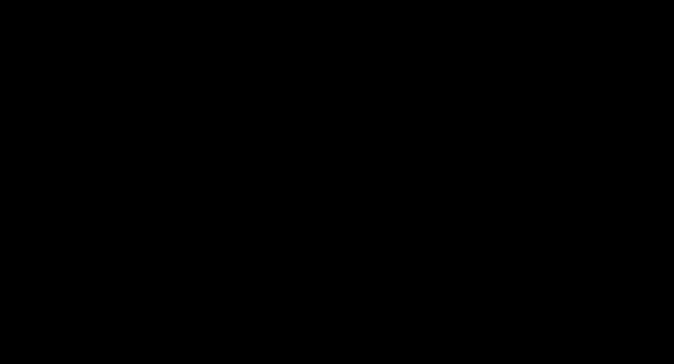
In large networks, their vast interconnectedness is a major factor contributing to the power of the brain. How do the functional properties of these networks emerge from their connectivity? Learning, an essential feature of the brain, is to a large extent associated with changes in that connectivity. What controls these biological processes, which can also involve the addition or removal of neurons? Computational modeling building on experimental observations is able to provide answers and insight. (Fig.3)

Much of the computational neuroscience research in ESAM is done in close collaboration with various experimental research groups; thus, ESAM students often are regular members also of their experimental partner group.

Core Faculty:
W.L. Kath, H. Riecke

Courtesy Faculty:
J. Fitzgerald

Return to Top