Research Areas

Mathematical Biology

Mathematical biology is expanding and developing rapidly as scientists in biological sciences turn from descriptive experiments to more quantitative experiments. The diversity and complexity of living organisms means there are vastly more challenges for mathematicians to explain and predict biological systems through modeling.

Mathematical biology is a broad topic that can cover a large range of length scales, from the submicron lengths of DNA polymers to the kilometer length scales of migration patterns of animal herds.

Jump to a Section

• Biofluid Mechanics
• Cancer
• Developmental Biology
• Genomics
• Microbiology
• Neuroscience
• Population Dynamics

Biofluid Mechanics

Biofluid mechanics is the subject of applying fundamental ideas from fluid mechanics to better understand the biology of living systems. This is a field that is moving very rapidly today because of the development of new experimental techniques that have allowed for quantitative measurements of specific biological systems, e.g., the motion of a cell.

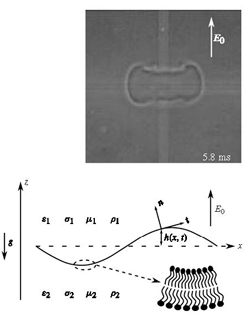
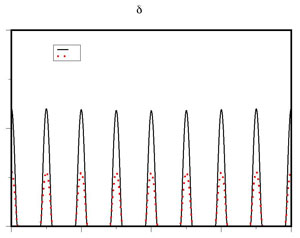
Research within ESAM involves the development of mathematical models of interesting biological systems, the development of new analytical and computational methods to solve these models, and interaction with experimental groups to verify the validity of the investigation. Specific areas of current research include biofilms (an aggregation of bacteria on solid surfaces surrounded by gas or liquid), vesicle and cell dynamics, and the dynamics of aneurysms.

Faculty

• Michael J. Miksis
• Petia Vlahovska

Return to Top

Cancer

Recent experimental techniques used to investigate biological systems are generating more and more amounts of data. Increasingly, researchers are turning to mathematical and computational models to understand this data, and to make quantitative predictions about how biological systems will behave in different conditions.

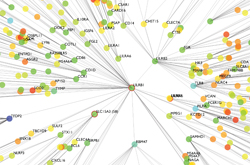
One example of this is the study of cancer. New models based, for example, upon the latest gene expression and high throughout sequencing data are producing new insights into some of the causes underlying this many-faceted disease.

Faculty

• William Kath

Return to Top

Developmental Biology

The correlation of organismal form and function is one of the central themes in biology, and the outcome of a developmental process—morphogenesis. While the zoo of organismal form seems limitless, we expect there to be unity in processes and mechanisms that give rise to them.

In analogy with the morphogenesis of our planet, while the details of the current shape of continents depends on time and historical contingency, the mechanisms that drive tectonic plates and the flows in the Earth's core are far more general. What are the underlying principles and mechanisms that drives the emergence of organismal form? This is the central question driving our research.

Our work explores two avenues of research: 1) Solving data-driven, inverse-problems that allow us to make measurements of physical forces and chemical kinetics that experiments do not give direct access, and 2) in close collaboration with experimentalists, we combine measurements made in their labs with ours to guide the development of mathematical models that are phenomenological in nature and formalize our intuition for how the physical properties of polymers, cells, and tissues emerges from, and constrains, the biological process of interest.

Faculty

• Madhav Mani
• Niall Mangan

Return to Top

Genomics

Having access to the genome of an organism is similar to having a primitive understanding of a language's alphabet without understanding what words mean and how sentences are structured. While there is no shortage of data flowing in from single-cell sequencing experiments, we are missing our Rosetta Stone to help make sense of it all.

This is perhaps the most pressing challenge in quantitative biology and biomedicine, and groups in ESAM are using tools from statistics, machine learning, and statistical physics to build data-driven mathematical models to address it.

Faculty

Madhav Mani

Return to Top

Microbiology

Microorganisms are complex systems unto themselves. They can exhibit significant adaptability to their environment caused by stresses such as starvation, competition from other species, or exposure to antibiotics. They are capable of locomotion, cell-to-cell communication, and coordination of both offensive and defensive strategies. The behavior of individual cells is regulated by expression of genes, which are often modeled by systems of ordinary differential equations. Often these systems incorporate elements of stochasticity to account for the non-determinant nature of these systems.

Colonies of microorganisms, taken as an aggregate, can be modeled using continuum models in the form of reaction-diffusion systems. These systems track the flow of nutrients and products in a larger environment.

Understanding microbiological systems is of critical importance to society. Most people are familiar with common pathogens that cause disease, but may not know that bacteria are also used to help clean waste water, produce household chemicals, and even produce energy. Mathematical modeling can aid in improving treatment of disease to reduce the possibility of antibacterial resistance and also streamline biochemical processes to improve energy or biochemical production beneficial to society.

Faculty

• David Chopp
• Niall Mangan

Return to Top

Neuroscience

With Periodic Research Animation, the amount of data available from experimental studies of the nervous system has grown, mathematical and computational models have become increasingly important for the understanding of brain function. Such models, for example, can explain and predict how the behavior of individual neurons is determined by their morphological structure and the multitude of ion channels present in the cells' membranes. These models help researchers explore how neurons process different types of inputs. They also provide the basis for detailed models involving networks of neurons. For such network models advanced computational techniques are essential.

It is also possible, however, to study many aspects of large networks of neurons using individual neuron models with substantially reduced complexity. For example, the propagation or failure of activity in neuronal networks with complex connectivity can be understood using relatively simple neuronal elements.

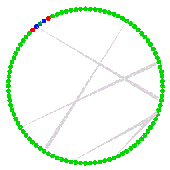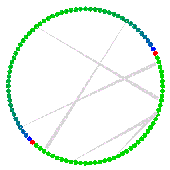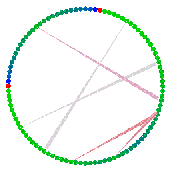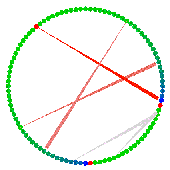
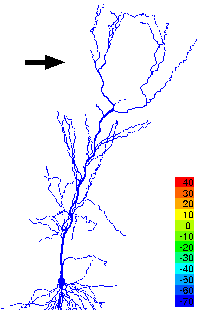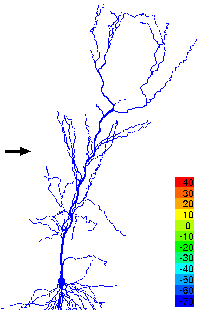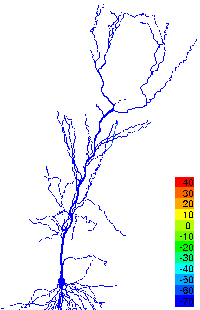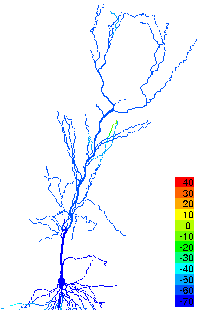
Problems such as these are being investigated by faculty and students within ESAM to understand the working of brain structures involved in the formation of memory and the processing of visual and olfactory information.

Faculty

• David Chopp
• William Kath
• Hermann Riecke

Return to Top

Population Dynamics

Many problems modeling the evolution of populations involve several different physical effects. These include:

• Birth and death rates as functions of the populations
• Intra-species competition, i.e., when the birthrate decreases as the population increases, due to crowding and competition for scarce resources
• Inter-species competition, when two or more species compete for the same resources
• Diffusive spreading
• Non-local interactions, i.e., the evolution of a population at a location depends not just on local conditions but also on resources in a neighborhood of the location

The result is a system of integro-partial differential equations, with the integral term modeling the effect of non-local interactions.

Faculty

• Alvin Bayliss
• Vladimir Volpert

Return to Top